Thermal stability problems and, consequently, explosive events may occur in the food industry, when organic powders are processed in equipment such as dryers, silos handling equipment, and filters
by Dante Marco De Faveri
16% of the explosive events involving dust in production plants ensured by the American FM Global in the years 1983-2006 occurred in the food industry, coming second after the wood industry. The extent, i.e. the consequences, of these events may be considerable, as they involve both the physical integrity of operators, and the integrity of installations and facilities. To estimate the effects, the reactivity of the material involved in the explosion should be known. As it is well-known, an explosion depends on several factors, among which, as in the case of powders, particle size and combustion heat deserve particular attention. In comparing different powders in terms of dangerousness, the combustion heat should be correlated with the amount of oxygen consumed in the explosive event. In fact, the gas phase into which the powder is dispersed, often contains a very limited amount of oxygen (with respect to the stoichiometric ratio), which determines how much heat is released per volume unit by the system involved in the explosion. As example, sucrose or starch develop a combustion heat of 470 kJ/mole of O2 consumed. The energy released, together with the fast developing of the event, determine the accidental magnitude, as shown in Table 1, which offers a synthesized report of explosion events occurred in agri-food industries over the last 25 years. The traditional protection systems for equipment that process flammable powders generally include: gas inerting and ignition sources removal; mixing with inert material; concentration of powders under the low flammability limit; explosion suppression; explosion proof vessels; explosion venting. The latter is the most widespread and economic technique. However, it is not effective for all types of installations, and it still needs more detailed knowledge and testing in order to be able to calculate generally valid algorithms according to the well-known “cubic law”. This law derives from many experimental tests conducted in big vessels (from a few to several tens of m3) and correlates the volume V of recipient, where the explosion occurs, with the maximum value of the pressure rate P with respect to temperature T, according to the equation:
Table 2 shows the average values for Kst (dust characteristic constant) for some foods in powder. It should be mentioned that values vary in a more or less wide range, depending on product composition and powder particle size. For example, the values expressed in 105 Pa m s-1, range between 58-130 for powder milk and 59-165 for sugar.
Intrinsically safe equipment
By neutralising, at least in part, the explosion risk related to a specific production process, it is possible to reduce the number of safety systems and to simplify control procedures. This makes the system intrinsically safe, as it is not dependent on control and safety devices; this also contributes to reduce human errors. The following presentation offers a review of devices used for processing powders, as for instance dryers. For the sake of simplicity, the dryers are divided in two main groups: completely mixed ones and unmixed ones. The first group, where temperature is uniformly distributed according to Semenov’s well-known theory, includes equipment operating in a fluidized bed; the second group collects those operations, where substances stored up in bulk, give origin to a non-uniform internal temperature system, according to Frank-Kamenetskii’s theory. Of great importance for the development and implementation of calculations, is the thermal analysis of runaway reactions typical of the present process, next to the determination of kinetic parameters which characterise them. Finally, whilst the approach presented here is generally valid, the proposed model is a verification criterion for equipment used in the the drying process used in the food industry.
Uniform internal temperature dryers
In a completely mixed system, like a fluidized bed, the turbulent regime inside the system ensures a uniform temperature distribution. In discontinuous dryers, the last step of the drying process is critical for the safety of the process, since temperature increases, while the heat exchange decreases. Considering that:
- The volumetric flow rate variation of air Q between input and output section is negligible;
- Even the result of the multiplication between absolute air humidity at input H1 and specific vapor heat cpv is negligible
And that at the last step of the drying process, the drying rate and the difference of absolute humidity between input and output drying gas tend to zero, the equation of heat balance may be written as follows:
This equation may be applied to the above mentioned conditions, but for safety purposes it also applies to the initial drying steps, since the adopted hypotheses are conservative for the purposes of design or corroborating calculations. By introducing Semenov’s criterion, under critical conditions, being DTcr = RT2/E, one can obtain the following expression for Q/V ratio (where V is the dryer’s volume):
Writing the heat generation term, the zero order hypothesis has been introduced, which is generally accepted by studying the divergent reactions, so that the term which refers to the concentration has been rejected. It follows that if ratios (Q/V)>(Q/V)cr, are kept, internal safety conditions of the apparatus will be guaranteed. This since the heat developed by eventual exothermic events would be soon removed by the air flow employed for drying, thus preventing or at least reducing the explosive event.
Non uniform internal temperature dryers
A substance layer (powder) inside a steady bed dryer, has been considered, which is limited by two infinite parallel planes at a distance 2r from each other, and touched by cooling fluid. Assuming that an exothermic reaction starts inside the layer, a relation between layer thickness and fluid characteristics (type, flow rate G, temperature T and exchange surface S) can be calculated so that the reaction could be maintained under control. By considering Tc the temperature at the layer center, To the outlet air/layer surface temperature, and X the spacial coordinate in the layer, from the center to the surface (Fig. 1), the surface temperature depends on the cooling fluid temperature Ta, and its behaviour can be obtained by setting the thermal balance of the heat developed by an undesired reaction and of the heat removed by the cooling fluid using the conservative hypothesis of zero order kinetic.
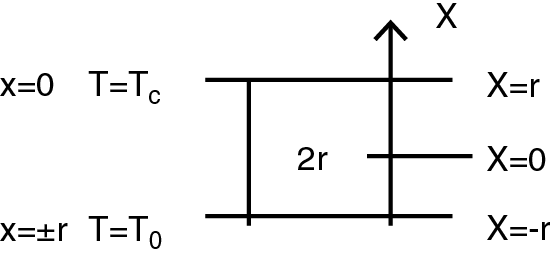
Since the system features a non uniform temperature distribution, for safety purposes in the generated heat equation, the value (Tc)max should be assumed. Furthermore, the maximum heat pre-explosive increase results from the geometry of the system which, in this case, is that of a plane geometry, equal to:
Hence, the heat balance between generated and removed heat, is:
being G the drying air flow rate. According to Frank Kamenetskii’s theory, the largest critical thickness rcr of the layer can be determined, below which reaction diverges.
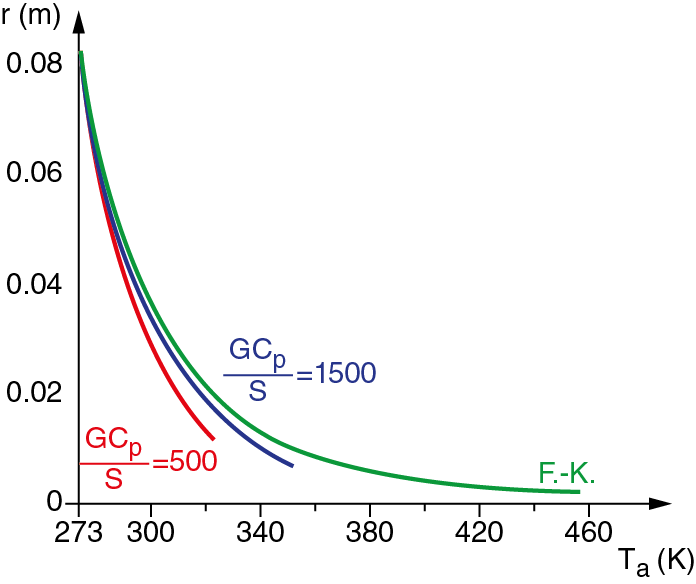
where dcr is Frank-Kamenetskii’s dimensionless parameter, which values 0.88 in the case of plane symmetry. For maximum temperature values of the powder layer, and hence, of the drying air (both maximum values are equal), the resulting solution is not an acceptable safety condition, because small alterations can cause an explosive development of the reaction. To find out the highest working temperature acceptable in terms of safety, both equations are combined, being V = 2rS, where V is the system volume and S the surface of the layer used for the heat exchange between material and air. The combination of the two previous equations gives a new equation, implicit in r, which can be found numerically, and which allows to find out the behaviour of critical thickness rcr, as a function of the cooling fluid temperature and of the Gcp/S ratio of the layer, below which the reaction does not diverge. Even in this case, by adopting an half thickness r > rcr, the process is kept internally safe, so that the removal of the heat exceeding from dried mass through thermal exchange with outside surrounding, is guaranteed. Fig. 2 shows as example the behaviour of critical thickness rcr as a function of the cooling fluid temperature Ta and of the parameter Gcp/S.
Conclusions
The proposed models allow correlating equipment size with process, plant and thermokinetic parameters of thermally unstable powders, which often occur in food industry. Hence, they can be considered as a design constraint or a criterion for consistency check, particularly useful for designers and operators. The proposed equations are suitable for the construction of simple and intrinsically safe systems, requiring minimum operative procedures with relevant minimum risks due to human errors, next to few controls, protection and safety devices. This agrees with the sector’s new trends, favouring the concept of inner safety as investment opportunity, rather than a cost, capable of relieving a company from extra expenses related to the mitigation of the adverse effects for human health and environment, deriving from protection, as long as obtained though sound innovative technologies.
Table 1 – Examples of dust explosions in the food industry
| Location | Event | Persons involved | ||
| Date | Dead | Injured | ||
| Namur (Belgium) | Explosion and fire at the automatic cereals silo. Caused by flame igniting dust. Nearby houses & factories were damaged in the series of blasts which followed. | 07/04/1993 | 4 | 7 |
| Geelong, Melbourne (Australia) | Dust explosion & fire when repair works being carried out on equipment at grain terminal. | 00/12/1993 | 0 | 0 |
| Blaye, Gironde (France) | Explosion in the central dust removal system of a cereals silo caused by mechanical impact or friction between impeller and stator. | 20/08/1997 | 12 | |
| Wichita, Kansas (USA) | Dust explosion at wheat elevator. Probably caused by a not correctly lubricated bearing of the conveyor belt. | 08/06/1998 | 7 | 10 |
| Campello sul Clitunno, Umbria (Italy) | Explosion of a silo containing olive oil, probably due to the presence of hexane vapours. The event occurred during maintenance interventions carried out by third-party. | 25/11/2006 | 4 | |
| Fossano, Piedmont (Italy) | Explosion of a mill during flour unloading from a tank. Probably caused by electrostatic charge accumulated in the rubber hose. It was followed by the explosion of the tank due to flour suspension. Material damages for hundreds of m. | 16/07/2007 | 5 | |
| Port Wentworth, Georgia (USA) | Explosion in a sugar factory, in the handling tunnel of the silos. Possible ignition of sugar dusts accumulated inside the tunnel, below the conveying system, due to metal parts overheating. | 07/02/2008 | 14 | 36 |
| Flagstaff, Arizona (USA) | Explosion of wheat powder in an elevator of the silos during maintenance interventions that involved hot work operations. | 14/09/2014 | 4 | |
| Table 2 – Average values of Kst for some food powders | ||||||
| Product | Kst (105 Pa m s-1) | |||||
| Coffee | 90 | |||||
| Caffein | 165 | |||||
| Dextrose | 18 | |||||
| Potato flour | 69 | |||||
| Fish flour | 35 | |||||
| Fructose | 102 | |||||
| Wheat | 112 | |||||
| Powder milk (skim) | 109 | |||||
| Lactose | 81 | |||||
| Rice | 190 | |||||
| Soy | 110 | |||||
| Tea | 68 | |||||
| Sugar | 82 | |||||


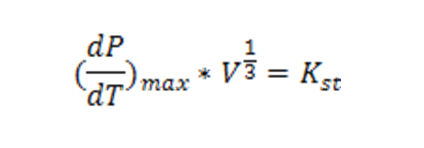
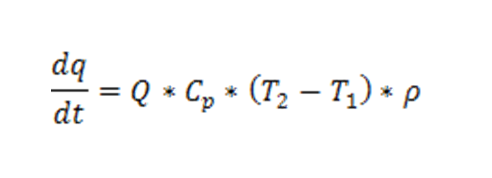
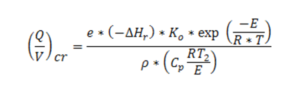
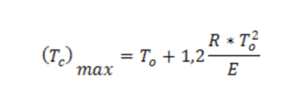
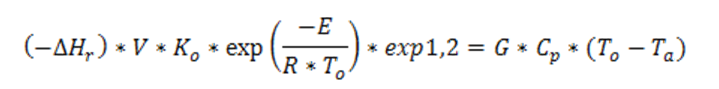
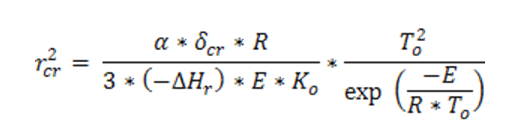



Public pressure on food processors to substantively reformulate foods and beverages using simpler, cleaner ingredients hasn’t missed the dairy aisle.
Comments are closed.